x
category_img
  • Home
  • Calculator 9 - Groundwater Mounding Calculator

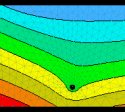
Calculator 9 - Groundwater Mounding Calculator

GROUNDWATER MOUND UNDER A RECTANGULAR RECHARGE AREA

Using the Hantush (1967) Derivation


Back to Calculators

The equation representing the groundwater mound beneath a rectangular recharge area is given by:

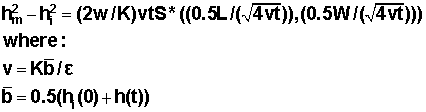
where hm is the maximum height of the mound; hi is the initial height of the water table; w is the recharge or percolation rate; K is the hydraulic conductivity; t is the time of interest; L and W are the length and width of the rectangular recharge area, and ε is the specific yield of the aquifer.  S* is an integral equation given by:

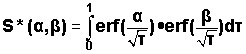
This equation is estimated in the calculator by using a table of values given by Hantush (1967).

GROUNDWATER MOUND UNDER A RECTANGULAR RECHARGE AREA 
Using the Hantush (1967) Derivation

Inputs

w (Percolation Rate):   [L/T]
K (Hydraulic Conductivity): [L/T]
S (Specific Yield): [-]
t (Time): [T]
hi (Initial Saturated Thickness): [L]
a (Length of Recharge Area): [L]
b (Width of Recharge Area): [L]

**KEEP UNITS CONSISTENT**

Results

**Note that because of estimations of an integral function, this is an estimate**

Maximum hydraulic head: [L]
Increase in hydraulic head: [L]

 

Hantush, M.S.(1967). Growth and Decay of Groundwater-Mounds in Response to Uniform Percolation, Water Resources Research vol. 3, no.1, pp 227-234.

Example:

What is the maximum mounding at the water table if 1000 liters/day of water is discharged on an area 3 x 4 m after 2 days (all water infiltrates). Given a hydraulic conductivity of 1 x10-6 m/s, and specific yield of 0.01 and an initial saturated thickness of 2 m.

Your results should yield a maximum hydraulic head of approximately 3.3 m and an increase in hydraulic head of 1.3 m.

What might have gone wrong?

- converting from 1000 liters/day to m/day.  Convert to m3/day using 1000 liters/m3, then divide by area to get the m/day of water infiltrating.  This value should be approximately 0.08 m/day

-converting the hydraulic conductivity to units of m/day. This value should be approximately 0.086

Summary

Inputs
w = 0.08 m/day, K = 0.086m/day, S=0.01, t = 2 days, hi = 2 m, a = 3m, b= 4 m

Results

Maximum hydraulic head = 3.3 m
Increase in hydraulic head = 1.3 m

 

 

 

 

You can also perform mounding calculations with graphical display using:

Hydrus
Saturated/Unsaturated Flow & Transport Model